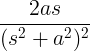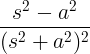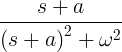Transformasi Laplace
- Fungsi transformasi Laplace
- Tabel transformasi Laplace
- Properti transformasi Laplace
- Contoh transformasi Laplace
Transformasi Laplace mengubah fungsi domain waktu menjadi fungsi domain s dengan integrasi dari nol hingga tak terbatas
dari fungsi domain waktu, dikalikan dengan e -st .
Transformasi Laplace digunakan untuk mencari solusi persamaan diferensial dan integral dengan cepat.
Penurunan domain waktu diubah menjadi perkalian dengan s dalam domain s.
Integrasi dalam domain waktu diubah menjadi divisi oleh s di domain s.
Fungsi transformasi Laplace
Transformasi Laplace didefinisikan dengan operator L {}:
![]()
Transformasi Laplace terbalik
Transformasi Laplace terbalik dapat dihitung secara langsung.
Biasanya transformasi terbalik diberikan dari tabel transformasi.
Tabel transformasi Laplace
| Nama fungsi | Fungsi domain waktu | Transformasi Laplace |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Konstan | 1 | |
| Linear | t | |
| Kekuasaan | t n |
|
| Kekuasaan | t a |
Γ ( a 1) ⋅ s - ( a 1) |
| Eksponen | e di |
|
| Sinus | berdosa di |
|
| Kosinus | cos di |
|
| Sinus hiperbolik |
sinh di |
|
| Kosinus hiperbolik |
cosh at |
|
| Tumbuh sinus |
t dosa di |
|
| Menumbuhkan kosinus |
t cos at |
|
| Sinus yang membusuk |
e -at sin ωt |
|
| Kosinus yang membusuk |
e -at cos ωt |
|
| Fungsi delta |
δ ( t ) |
1 |
| Delta tertunda |
δ ( ta ) |
e -as |
Properti transformasi Laplace
| Nama properti | Fungsi domain waktu | Transformasi Laplace | Komentar |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Linearitas | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b konstan |
| Perubahan skala | f ( at ) |
|
a / 0 |
| Bergeser | e -at f ( t ) | F ( s + a ) | |
| Menunda | f ( ta ) | e - sebagai F ( s ) | |
| Penurunan |
|
sF ( s ) - f (0) | |
| Derivasi ke-N |
|
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Kekuasaan | t n f ( t ) |
|
|
| Integrasi |
|
|
|
| Timbal-balik |
|
|
|
| Lilitan | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * adalah operator konvolusi |
| Fungsi periodik | f ( t ) = f ( t + T ) |
|
Contoh transformasi Laplace
Contoh 1
Temukan transformasi dari f (t):
f ( t ) = 3 t + 2 t 2
Larutan:
ℒ { t } = 1 / dtk 2
ℒ { t 2 } = 2 / dtk 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Contoh # 2
Temukan transformasi kebalikan dari F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Larutan:
Untuk menemukan transformasi invers, kita perlu mengubah fungsi domain s menjadi bentuk yang lebih sederhana:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Untuk mencari a dan b, kita mendapatkan 2 persamaan - salah satu koefisien s dan kedua sisanya:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Sekarang F (s) dapat diubah dengan mudah dengan menggunakan tabel transformasi untuk fungsi eksponen:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Lihat juga
Advertising
KALKULUS
- Membatasi
- Turunan
- Integral
- Seri
- Transformasi Laplace
- Lilitan
- Simbol kalkulus
TABEL CEPAT