Staðalfrávik

Í líkindum og tölfræði er staðalfrávik handahófsbreytu meðalvegalengd handahófskenndrar breytu frá meðalgildinu.

Það táknar hvernig handahófi breytunni er dreift nálægt meðalgildinu. Lítið staðalfrávik gefur til kynna að tilviljanakenndri breytu sé dreift nálægt meðalgildinu. Stór staðalfrávik gefur til kynna að tilviljanakenndri breytu sé dreift langt frá meðalgildinu.

Formúlu skilgreiningar á staðalfráviki

Staðalfrávikið er kvaðratrót dreifni handahófsbreytu X, með meðalgildið μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Frá skilgreiningu á staðalfráviki sem við getum fengið

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Staðalfrávik samfellds handahófsbreytu

Fyrir samfellda slembibreytu með meðalgildi μ og líkindarþéttni f (x):

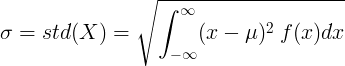
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

eða

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Staðalfrávik stakrar handahófsbreytu

Fyrir stakan handahófsbreytu X með meðalgildi μ og líkindamassafall P (x):

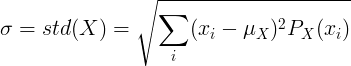
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

eða

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Líkindadreifing ►

 

Sjá einnig

Advertising

Líkindi og tölfræði
HRAÐ TÖFLUR