Интегрален

Интеграцијата е обратна операција на изведувањето.

Интеграл на функција е област под графиконот на функцијата.

Неопределена интегрална дефиниција

Кога dF (x) / dx = f (x) =/ интеграл (f (x) * dx) = F (x) + c

Неопределени интегрални својства

интеграл (f (x) + g (x)) * dx = интеграл (f (x) * dx) + интеграл (g (x) * dx)

интеграл (a * f (x) * dx) = a * интеграл (f (x) * dx)

интеграл (f (a * x) * dx) = 1 / a * F (a * x) + c

интеграл (f (x + b) * dx) = F (x + b) + c

интеграл (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

интеграл (df (x) / dx * dx) = f (x)

Промена на променливата на интеграција

Когаx = g (t) иdx = g '(t) * dt

интеграл (f (x) * dx) = интеграл (f (g (t)) * g '(t) * dt)

Интеграција по делови

интеграл (f (x) * g '(x) * dx) = f (x) * g (x) - интеграл (f' (x) * g (x) * dx)

Табела со интеграли

интеграл (f (x) * dx = F (x) + c

интеграл (a * dx) = a * x + c

интеграл (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, кога a </ - 1

интеграл (1 / x * dx) = ln (апс (x)) + в

интеграл (e ^ x * dx) = e ^ x + c

интеграл (a ^ x * dx) = a ^ x / ln (x) + c

интеграл (ln (x) * dx) = x * ln (x) - x + c

интеграл (sin (x) * dx) = -cos (x) + c

интеграл (кос (х) * дх) = грев (х) + в

интеграл (тен (x) * dx) = -ln (апс (cos (x))) + в

интеграл (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

интеграл (лакови (x) * dx) = x * лакови (x) - sqrt (1-x ^ 2) + c

интеграл (арктан (x) * dx) = x * арктан (x) - 1/2 * ln (1 + x ^ 2) + c

интеграл (dx / (ax + b)) = 1 / a * ln (апс (a * x + b)) + c

интеграл (1 / кварт (a ^ 2-x ^ 2) * dx) = арцин (x / a) + c

интеграл (1 / кварт (x ^ 2 + - a ^ 2) * dx) = ln (апс (x + sqrt (x ^ 2 + - a ^ 2)) + c

интеграл (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

интеграл (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * арктан (x / a) + c

интеграл (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (апс (((a + x) / (ax))) + c

интеграл (sinh (x) * dx) = cosh (x) + c

интеграл (cosh (x) * dx) = sinh (x) + c

интеграл (тан (x) * dx) = ln (cosh (x)) + в

 

Дефинитивна интегрална дефиниција

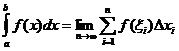
интеграл (a..b, f (x) * dx) = lim (n-/ inf, збир (i = 1..n, f (z (i)) * dx (i))) 

Когаx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Дефинитивна интегрална пресметка

Кога ,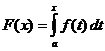

 dF (x) / dx = f (x) и

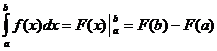
интеграл (a..b, f (x) * dx) = F (b) - F (a) 

Одредени интегрални својства

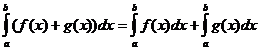
интеграл (a..b, (f (x) + g (x)) * dx) = интеграл (a..b, f (x) * dx) + интеграл (a..b, g (x) * dx )

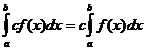
интеграл (a..b, c * f (x) * dx) = c * интеграл (a..b, f (x) * dx)

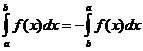
интеграл (a..b, f (x) * dx) = - интеграл (b..a, f (x) * dx)

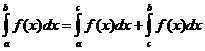
интеграл (a..b, f (x) * dx) = интеграл (a..c, f (x) * dx) + интеграл (c..b, f (x) * dx)

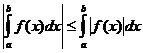
апс (интеграл (a..b, f (x) * dx)) <= интеграл (a..b, апс (f (x)) * dx)

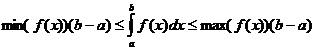мин (f (x)) * (ba) <= интеграл (a..b, f (x) * dx) <= max (f (x)) * (ba) когаx член на [а, б]

Промена на променливата на интеграција

Когаx = g (t) ,dx = g '(t) * dt ,g (алфа) = a ,g (бета) = b

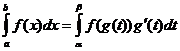
интеграл (a..b, f (x) * dx) = интеграл (алфа..бета, f (g (t)) * g '(t) * dt)

Интеграција по делови

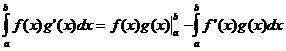
интеграл (a..b, f (x) * g '(x) * dx) = интеграл (a..b, f (x) * g (x) * dx) - интеграл (a..b, f' (x) * g (x) * dx)

Теорема на средна вредност

Кога f ( x ) е континуирано, постои точкаc е член на [a, b] така

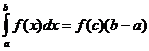
интеграл (a..b, f (x) * dx) = f (c) * (ba)  

Трапезоидна приближување на определен интеграл

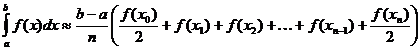
интеграл (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. + f (x (n-1)) + f (x (n)) / 2)

Гама функција

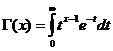
гама (x) = интеграл (0..inf, t ^ (x-1) * e ^ (- t) * dt

Гама функцијата е конвергентна за x/ 0 .

Карактеристики на гама функцијата

G ( x +1) = x G ( x )

G ( n +1) = n ! , кога n ℕ (позитивен цел број).е член на

Функцијата Бета

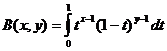
B (x, y) = интеграл (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Бета функција и врска со гама функција

Б (x, y) = Гама (x) * Гама (y) / Гама (x + y)

 

Advertising

 

 

ПРЕСМЕТ
БРЗИ ТАБЕЛИ